

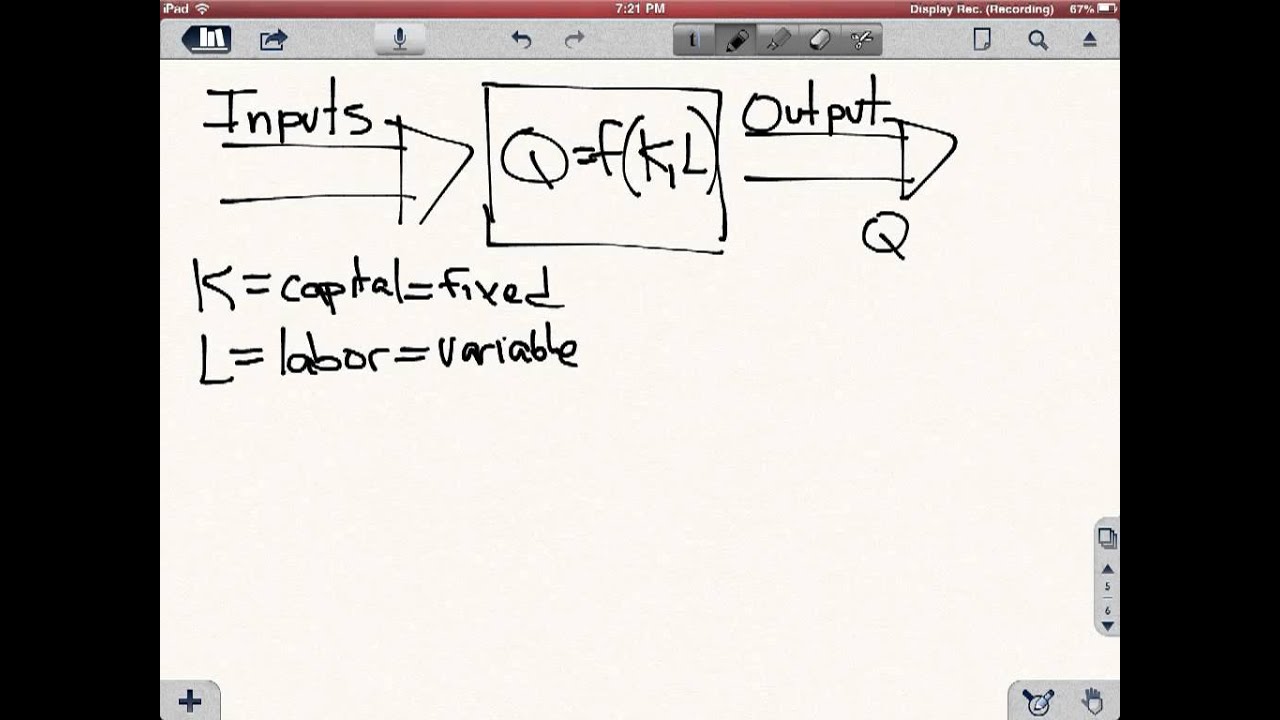
The cookie is used to store the user consent for the cookies in the category "Other. This cookie is set by GDPR Cookie Consent plugin. The cookies is used to store the user consent for the cookies in the category "Necessary". The cookie is set by GDPR cookie consent to record the user consent for the cookies in the category "Functional". The cookie is used to store the user consent for the cookies in the category "Analytics". These cookies ensure basic functionalities and security features of the website, anonymously. Necessary cookies are absolutely essential for the website to function properly. The short-run production function can be mathematically expressed as follows:

Therefore, on the basis of time period, production function can be classified in two types, namely, short-run production function and long-run production function. On the other hand, in the long- run, the organization can increase labor and capital both for increasing the level of production. In such a case, the organization only increases labor to increase the level of production. In short-run, the supply of capital is inelastic (except for individual organization in perfect competition). On the basis of time period required to increase production, an organization decides whether it should increase labor or capital or both.Īn organization takes into account either long- run production or short-run production for increasing the level of production. The production of diamonds would increase with the increase in labor and capital. I leave the actual derivation of the aggregate production function as an exercise.This production function implies that quantity of diamond production depends on labor engaged in producing diamond and capital required to carry out production. Due to DRS, this necessarily means that both $k_1, k_2 > 0$. You will want to split up capital between the two firms such that marginal returns equalize: $k_1, k_2 : F_1'(k_1) = F_2'(k_2)$.
Now, it won't be the case that one firm is more productive than the other one always. If one cook can bake one cake with each egg, and the other cook can also bake one cake with each egg, then the two cooks together can bake two cakes with each egg? Decreasing returns to scale If you think that adding them up makes sense, you're not thinking things through: The solution here is $G(l,k) = A_1F(k, l) $ if $A_1 > A_2$, and vice-versa. That is, define $G(l, k)$ as the aggregate production function.
This is because of CRS (which indeed means that as you scale up one production function, it's marginal product will always be larger than the other one's). As one is more efficient, it will get more inputs.Īnd what is the maximum? Give all of the inputs to the more productive firm. He will want to equalize marginal returns across the firms. Here we can solve the social planner's problem (why?) instead of looking at a competitive equilibrium. Both have the same curvature (and are CRS), but one is more productive. Consider two firms with production functions $A_1 F(k,l)$ and $A_2 F(k,l)$.


 0 kommentar(er)
0 kommentar(er)
